 |
www.elektronik.si
Forum o elektrotehniki in računalništvu
|
| Poglej prejšnjo temo :: Poglej naslednjo temo |
| Avtor |
Sporočilo |
Drago_G
Član

Pridružen-a: Ned 12 Dec 2010 15:12
Prispevkov: 288
Aktiv.: 1.62
Kraj: Primorska
|
 Objavljeno: Tor Apr 16, 2013 12:09 am Naslov sporočila: matematično-programerski problem Objavljeno: Tor Apr 16, 2013 12:09 am Naslov sporočila: matematično-programerski problem |
 |
|
Pozdravljeni!
Upam, da nisem preveč zgrešil teme.
Imam en zanimiv matematično programerski problem.
Pogoj: zadeva mora biti narejena v Wolfram Mathematica 6.0 (licenca), drugi podobni programi odpadejo (recimo Matlab,...) zaradi investicije. Le v opombo, da ne bodo leteli podobni dobronamerni nasveti. Seveda ni potrebno natančne sintakse, to bom sam uredil. Sam bi rad videl, če mi lahko pomagate le matematično rešiti naslednji problem.
Imam 2 kroga s polmerom R0, ki sta medsebojno oddaljena za razdaljo d (od središča prvega do središča drugega). Ta 2 kroga moram zapolniti z tokovnimi nitmi (ve slučajno kdo njihovo angleško ime?), ki so v bistvu manjši krogci s polmerom r1 (r1 je pri vseh krogcih fiksen, je pa odvisen od drugih spremenljivk).
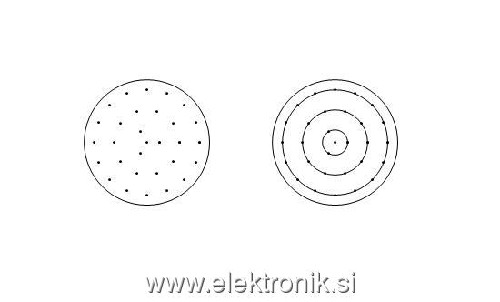
V bistvu pride n takšnih krogcev polmera rniti (n/2 v vsakem od krogov), ki imajo svoje središče. Več je razvidno iz slike1, ki je priložena.
Moj problem pa je, kako matematično zapisati središča teh krogcev v obliki (x, y) v dva vektorja-X in Y (???) ("table" v Mathematici). Seveda mora biti zapis takšen, da se generira samodejno, če spremenimo r1 ali R0 ali katerokoli spremenljivko, od katerih sta ta dva izraza odvisna.
V glavnem, doslej mi je uspelo stvar zapisati za fiksen primer. Glej slika2.
Sam krog sem razdelil v določeno število "stolpcev" po formuli: stevilovrstic = Round[2*R0/(2*rniti)]
Nato sem dobil toliko notranjih krogov (glej desno polovico slike2, kjer so narisani), na katere sem fiksiral središča
tokovnih niti (malih krogcev, na sliki so njihova središča označena s piko).
Formula, ki sem jo uporabil za ta izris je:
Table[{(R0 - rniti)*Cos[tocka] + d/2, (R0 - rniti)*Sin[tocka]}, {tocka, 0, 2 \[Pi], 2*Pi/steviloniti1}]]
Zgornja formula je konkretno za skrajno zunanje niti, za druge pa sem uporabil drug zapis, recimo (R0-3*rniti)* ...
Ker pa se bo število "vrstic oziroma stolpcev spreminjalo", bi potreboval drug, bolj avtomatičen zapis teh točk s
pomočjo if, while,... zank. Seveda pa morajo biti x komponente točk v enem "vektorju", y komponente pa v drugem.
Bi mi lahko kdo svetoval, kako naj se lotim zadeve.
Prvič moram najverjetneje ugotoviti v katerem krogu se nahaja posamezna nit-ali v desnem ali levem.
Torej nekako takole: če je i<= n/2, potem je v levem krogu, sicer v desnem
If [i<=n/2, stavek1, stavek2, {i, n}]
Problem pa je kako sedaj zastaviti stavek1 in posledično podobno tudi stavek2.
Mi zna kdo pomagati vsaj teoretično?
Upam, da nisem z besedilom preveč zakompliciral, sicer so slike. Rad bi matematično zapisal x koordinate točk (ki so označene na sliki2) v en vektor in y koordinate teh istih točk v drug vektor, vse to neglede na število teh točk.
Hvala za pomoč
| Opis: |
|
| Velikost datoteke: |
10.94 KB |
| Pogledana: |
7 krat |
|
| Opis: |
|

Download |
| Ime datoteke: |
slika1.jpg |
| Velikost datoteke: |
17.51 KB |
| Downloadano: |
12 krat |
|
|
| Nazaj na vrh |
|
 |
snow
Član


Pridružen-a: Tor 27 Dec 2005 14:02
Prispevkov: 341
Aktiv.: 1.44
Kraj: Ljubljana || Velenje
|
 Objavljeno: Tor Apr 16, 2013 9:52 am Naslov sporočila: Objavljeno: Tor Apr 16, 2013 9:52 am Naslov sporočila: |
 |
|
Dajmo se pogovarjat recimo samo o krožnicah in malih krogih.
Torej ti bi rad na krožnice, katerih radij se zmanjšuje dajal gor manjše kroge?
| Citiram: |
| Sam krog sem razdelil v določeno število "stolpcev" po formuli: stevilovrstic = Round[2*R0/(2*rniti)] |
Kakšne vrstice in stolpci?
Ta formula je za število malih krogcev na posamezno krožnico?
Koordinate malih krogov so za oba kroga glede na center enake?
Računaj malih krogov za eno krožnico, za drugo pa samo x-u prišteješ/odšteješ d, za vsako središče malega kroga.
V končni fazi, ko imaš vektor X1 in Y1 za prvi krog, na koncu za drugi krog narediš samo:
X2 = X1 + d
Y2 = Y1
|
|
| Nazaj na vrh |
|
 |
Drago_G
Član

Pridružen-a: Ned 12 Dec 2010 15:12
Prispevkov: 288
Aktiv.: 1.62
Kraj: Primorska
|
 Objavljeno: Tor Apr 16, 2013 11:26 am Naslov sporočila: Objavljeno: Tor Apr 16, 2013 11:26 am Naslov sporočila: |
 |
|
OK, poenostavimo problem le na krožnice in male kroge. Prav tako lahko vzamemo le en "velik" krog, saj tu ni problema preseliti dogajanja na drugi krog.
Torej vzemimo sliko2 in glejmo le desni krog.
V "veliki" krog s polmerom R0 postavimo male kroge s polmerom r1. Ker pa niti R0, niti r1 nista vedno enaka, bi potreboval "avtomatsko" formulo (nekaj z for, if, while,.. zankami), ki bi mi razporedila središča malih krogov tako, kot so na desni strani (ali na levi, saj je enako) slike2.
Pogoj je le, da so vsi mali krogi s polmerom r1 znotraj velikega kroga s polmerom R0 ter da se medsebojno ne prekrivajo. Torej njihovo število ni fiksno, temveč je odvisno od r1 in R0 (ki sta odvisna od drugih stvari).
V glavnem, imam dva problema:
1) v koliko obročih (vrstah) bodo ti mali krogci okrog središča velikega kroga
2) koliko malih krogov bo na enem obroču.
Podana pa sta:
R0=polmer velikega kroga
r1=polmer malih krogcev. R1 je pravzaprav maksimalen polmer malih krogcev, dejanski polmer malih krogcev je lahko manjši. Vendar naj bo čimbližji r1, da dobim čimmanj točk.
Upam, da je sedaj moj problem kaj bolj jasen. Hvala za pomoč.
_________________
Neumnih vprašanj ni, so le neumni odgovori |
|
| Nazaj na vrh |
|
 |
igo
Član

Pridružen-a: Sre 11 Okt 2006 19:11
Prispevkov: 3641
Aktiv.: 15.96
|
 Objavljeno: Tor Apr 16, 2013 12:50 pm Naslov sporočila: Objavljeno: Tor Apr 16, 2013 12:50 pm Naslov sporočila: |
 |
|
Vedeti moraš, na katerih polmerih so niti (erniti) in na katerih kotih so niti (finiti).
Potem dobiš 2D vektor x(erniti, finiti) in 2D vektor y(erniti, finiti) , kjer so središča niti.
Za drugi krog pa x od središč prišteješ d, da dobiš 2D vektor xx(erniti, finiti).
Število členov vektorjev se izračuna sproti iz R1 in R0.
Naj bo snvp SteviloNitiVPlasti celoštevilski količnik obseg(erniti)/R1 , a ga izračunaš šele v for zanki.
c1 in c2 sta faktorja polnjenja ali česa podobnega.
Začetek
določiš R0, R1, c1, c2, d
SteviloPlastiNiti stpn = celostevilski količnik (R0+c1)/(R1+c2).
for erniti= 1 to stpn @ r na katerih so niti
snvp = 2*Pi*erniti /R1 @ koliko je niti v plasti
for finiti= 0 to snvp
x(erniti,finiti)=erniti*R1*sin(360*finiti/snvp)
xx(erniti,finiti)= d + x(erniti, finiti)
y(erniti,finiti)=erniti*R1*cos(360*finiti/snvp)
end for
end for
y so skupni, x in xx sta pa 2 kroga.
Malo poštimaj sintakso, a to naj bi bilo to.
Če moraš pa najprej določiti število členov v vektorju, najprej izračunaš, koliko bo plasti, nato pa največji obseg deliš z obsegom ene niti. c1 in c2 sta zato, ker se sosednje niti ne dotikajo na skrajnih merah.
_________________
Teoretično je praksa posledica teorije, praktično je pa ravno obratno. (igo 2001)
LP, Igor |
|
| Nazaj na vrh |
|
 |
snow
Član


Pridružen-a: Tor 27 Dec 2005 14:02
Prispevkov: 341
Aktiv.: 1.44
Kraj: Ljubljana || Velenje
|
 Objavljeno: Tor Apr 16, 2013 12:56 pm Naslov sporočila: Objavljeno: Tor Apr 16, 2013 12:56 pm Naslov sporočila: |
 |
|
Število krožnic (torej kolobar debeline 2*R1) znotraj velikega kroga je
| Koda: |
| N0=Floor[R0/(2 R1)] |
zaokroženo navzdol. Tale del ni optimalen, ker lahko krogi iz ene krožnice segajo v področje krogov iz druge krožnice... ampak potem smo pri težjih problemih 
In potem, za vse krožnice zračunamo njihove polmere in število krogov na teh krožnicah in njihove koordinate popakiramo v X in Y:
| Koda: |
X = {};
Y = {};
For[i = 1, i <= N0, i++,
K0 = R0 - (2 i - 1)*R1; (*radij kroznice*)
N1 = Floor[2 Pi K0/(2 R1)]; (*stevilo krogov na kroznici*)
For[kot = 0, kot < 2 Pi, kot += 2 Pi/N1,
AppendTo[X, K0*Cos[kot]];
AppendTo[Y, K0*Sin[kot]]
];
];
Print[X, Y]
|
Pa izračun števila krogov je bolj približen...
Če pa ne rabiš tega po krožnicah, vzami trenutno najboljše znana pakiranja: http://hydra.nat.uni-magdeburg.de/packing/cci/
|
|
| Nazaj na vrh |
|
 |
igo
Član

Pridružen-a: Sre 11 Okt 2006 19:11
Prispevkov: 3641
Aktiv.: 15.96
|
 Objavljeno: Tor Apr 16, 2013 4:00 pm Naslov sporočila: Objavljeno: Tor Apr 16, 2013 4:00 pm Naslov sporočila: |
 |
|
Zdajle sem opazil, da sem polmere drugače označil.
V mojih formulah je
- R0 zunanji polmer kabla
- R1 polmer ene niti
_________________
Teoretično je praksa posledica teorije, praktično je pa ravno obratno. (igo 2001)
LP, Igor |
|
| Nazaj na vrh |
|
 |
Drago_G
Član

Pridružen-a: Ned 12 Dec 2010 15:12
Prispevkov: 288
Aktiv.: 1.62
Kraj: Primorska
|
 Objavljeno: Tor Apr 16, 2013 11:36 pm Naslov sporočila: Objavljeno: Tor Apr 16, 2013 11:36 pm Naslov sporočila: |
 |
|
Najlepša hvala obema, mi je kar žal da si nisem pomoči poiskal prej, ko pa imamo toliko znanja na kupu na tem forumu.
Danes žal nisem imel veliko časa, tako da sem le delno pogledal situacijo.
Igo, tvojo formulo oziroma opis formule sem zaenkrat pustil v rezervi, saj se ne bi rad igral še s faktorji polnitve.
Sem raje uporabil snow-ovo formulo, ki je na prvi pogled to, kar rabim (ali je to res, bom videl ob nadaljnem delu). Vektorja X in Y sem združil v obliko {x1, y1}, {x2, y2},... s pomočjo ukaza Transpose, ter izrisal graf. Ko sem združil graf točk in krožnico velikega kroga, sem dobil to, kar mislim da želim.
Jutri pa z delom naprej. Najprej dodati še drugi krog, nato pa mučit podatke.
Hvala obema za pomoč, ne izključujem možnosti da se bom v zvezi s tem vprašanjem še kdaj oglasil. LP
_________________
Neumnih vprašanj ni, so le neumni odgovori |
|
| Nazaj na vrh |
|
 |
Drago_G
Član

Pridružen-a: Ned 12 Dec 2010 15:12
Prispevkov: 288
Aktiv.: 1.62
Kraj: Primorska
|
 Objavljeno: Tor Apr 23, 2013 11:56 pm Naslov sporočila: Objavljeno: Tor Apr 23, 2013 11:56 pm Naslov sporočila: |
 |
|
Spet potrebujem malo pomoči, da se prebijem skozi problem.
Imam dve matriki.
Matrika polozaj vsebuje koordinate točk v X in Y osi.
Matrika izracun vsebuje izračunan podatek za vsak položaj iz prejšnje matrike.
Se pravi:
polozaj=[x1, y1; x2, y2; ... ; xn, yn]
izracun=[A1; A2; ...; An]
Matrike izračun pa ne morem preprosto izračunati iz matrike položaj po formuli f=f(x,y).
Moj problem je:
Kako narisati 2D sliko/graf na kateri bi barvno prikazal podatek iz matrike izračun na položaju iz matrike položaj.
Torej recimo da imam v matriki izračun podatke od -5 do 5, ki bi jih rad prikazal z barvami od rdeče do modre (ali kaj podobnega) za vse točke, podane v matriki položaj.
Drugo vprašanje je, kako bi na sliki prikazal vmesne točke med dvema točkama, tako da bi program izračunal vmesno vrednost (da dobim videz zveznosti).
Pogoj za vse to je seveda program Mathematica 6.0
Upam, da kdo zna pomagati ali vsaj svetovati kako naprej. Hvala za pomoč.
LP
_________________
Neumnih vprašanj ni, so le neumni odgovori |
|
| Nazaj na vrh |
|
 |
igo
Član

Pridružen-a: Sre 11 Okt 2006 19:11
Prispevkov: 3641
Aktiv.: 15.96
|
 Objavljeno: Sre Apr 24, 2013 9:10 am Naslov sporočila: Objavljeno: Sre Apr 24, 2013 9:10 am Naslov sporočila: |
 |
|
| Koda: |
A = {};
For[i = 1, i <= SteviloStolpcev, i++,
For[j = 1, j <= SteviloVrstic, j++,
A(i,j)= X(i,j) + - * / Y(i,j)
];
];
Potem obstaja ukaz za izris vrednosti A(i,j), ki ima spodaj i-os in j-os, po višini pa vrednost A v tisti točki. Dobljena ploskev že ima sosednje vrednosti A med seboj zvezno povezane in mavrično pobarvano od min(A) do max(A).
|
Drugače pa loči XY(i,j) matriko, da boš imel v eni samo X(i,j) in v drugi samo Y(i,j). Potem iz njiju izračunaš A(i,j).
Dodano: Če imaš samo vektorja x(1...n) in y(1...n), bodo tudi vsi A(1...n). Torej na krivulji.
Če bi rad dobil ploskev, A(i,j), kjer gresta i in j do n (SteviloVrstic = n , SteviloStolpcev = n), sem pa že zgoraj napisal.
_________________
Teoretično je praksa posledica teorije, praktično je pa ravno obratno. (igo 2001)
LP, Igor |
|
| Nazaj na vrh |
|
 |
Drago_G
Član

Pridružen-a: Ned 12 Dec 2010 15:12
Prispevkov: 288
Aktiv.: 1.62
Kraj: Primorska
|
 Objavljeno: Sob Maj 04, 2013 11:31 pm Naslov sporočila: Objavljeno: Sob Maj 04, 2013 11:31 pm Naslov sporočila: |
 |
|
Po dolgem času se spet oglašam. Žal so imele druge stvari prioriteto pred tem, tako da se s tem nisem ukvarjal. Sedaj pa ponovno k stvari, problem je zame še vedno nerešljiv.
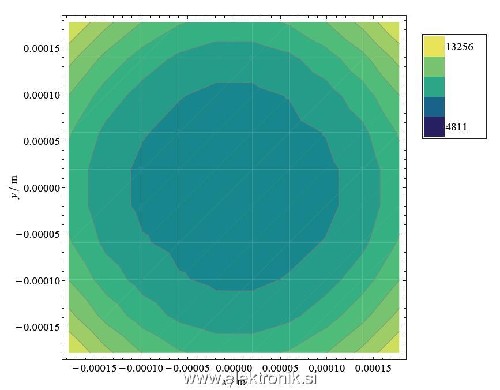
Mogoče smo se narobe razumeli, mogoče jaz narobe razumem. Želel bi imeti podoben graf, kot na priloženi sliki, le da bi imel za okvir krog (polmer R0-polmer okroglega vodnika) in ne kvadrat. Koordinate notranjih točk so podane v X in Y, vrednost v podani točki je zapisana v tretji matriki (vektorju, list ali karkoli že je to).
Vmesne vrednosti bi rad preprosto interpoliral.
Zatakne pa si mi pri izrisu grafa, saj mi nobena od možnosti ne ustreza. ListContourPlot ali ContourPlot se mi zdita še najbolj uporabna, a iz njih ne zmorem nič pametnega povleči. Prilagajam še mojo kodo za pomoč (se opravičujem za neurejenost kode, ni še končna verzija).
PS: program je mathematica 6.0
Že v naprej hvala za pomoč
| Opis: |
|
| Velikost datoteke: |
46.8 KB |
| Pogledana: |
1 krat |
|
| Opis: |
|

Download |
| Ime datoteke: |
ve15.rar |
| Velikost datoteke: |
130.51 KB |
| Downloadano: |
1 krat |
|
|
| Nazaj na vrh |
|
 |
igo
Član

Pridružen-a: Sre 11 Okt 2006 19:11
Prispevkov: 3641
Aktiv.: 15.96
|
 Objavljeno: Ned Maj 05, 2013 12:41 pm Naslov sporočila: Objavljeno: Ned Maj 05, 2013 12:41 pm Naslov sporočila: |
 |
|
Okrogel graf lahko nastane kvečjemu pri uporabi polarnega koordinatnega sistema. V Helpu išči Polar ... in preberi teme, ki vsebujejo to besedo.
Če imaš točke(x,y), jih pretvori v točke(r,fi).
Enako stori še za vrednosti v tistih točkah.
| Koda: |
for [x=0 , x <= n , x++
for [y=0 , y <= n , y++
Vxy = Vrednost(x,y)
r = koren( x^2 + y^2 )
fi = ArcSin( y / r ) = ArcCos( x / r )
zaokrožitev r in fi na par decimalk
množenje r in fi, da bosta brez decimalk
nastala bosta celoštevilska R in FI
Vrednost(R,FI) = Vxy
];
]; |
Boš pa iz celoštevilskih x in y dobil čudo in pol na mnogo decimalk, zato bi moral r in fi nekako zaokrožiti na končno število možnih R in Fi, da dobiš indeksirane Vrednost(R,FI).
Pa na telefonu mi .rar ne odpre. Če ni prevelika datotfka, prilepi .pdf ali .txt .
_________________
Teoretično je praksa posledica teorije, praktično je pa ravno obratno. (igo 2001)
LP, Igor |
|
| Nazaj na vrh |
|
 |
Drago_G
Član

Pridružen-a: Ned 12 Dec 2010 15:12
Prispevkov: 288
Aktiv.: 1.62
Kraj: Primorska
|
 Objavljeno: Ned Maj 05, 2013 3:47 pm Naslov sporočila: Objavljeno: Ned Maj 05, 2013 3:47 pm Naslov sporočila: |
 |
|
Hvala za pomoč Igo.
Prilagajam pdf, če ti bo kaj bolj v pomoč. Sicer pa mislim, da je večji problem kako vrednosti iz 3 matrike pretvoriti v graf (ta naj bo barvni 2D, podoben kot v priloženi prilogi v prejšnjem sporočilu), kot pa doseči okrogel graf.
Okrogel graf bi verjetno dosegel tudi z if stavkom v katerem bi dodal pogoj, da je točka znotraj kroga s polmerom R0.
Torej nekako takole (sintaksa pisana na pamet):
If (točka=znotraj kroga R0, točka=..., drugače točka=0)
Čeprav tudi polarni graf je možnost, samo mislim, da kompliciramo.
Urejanje: Da bo jasno. Imam 3 podatke:
X
Y
toki
Vsi trije imajo enako število elementov (trenutno 58, toda to število ni fiksno), na grafu pa bi rad imel tako:
v točki (x1, y1) je vrednost tok1, v točki (x2, y2) je vrednost tok2, ...
Torej diagram z x na vodoravni osi, y na navpični osi ter tok prikazan barvno, glede na vrednost v tej točki.
Med točkami pa bi bile vrednosti tokov interpolirane, toda to je že nadgradnja problema.
Hvala za pomoč.
| Opis: |
|

Download |
| Ime datoteke: |
ve15.pdf |
| Velikost datoteke: |
240.06 KB |
| Downloadano: |
5 krat |
|
|
| Nazaj na vrh |
|
 |
|
|
Ne, ne moreš dodajati novih tem v tem forumu
Ne, ne moreš odgovarjati na teme v tem forumu
Ne, ne moreš urejati svojih prispevkov v tem forumu
Ne, ne moreš brisati svojih prispevkov v tem forumu
Ne ne moreš glasovati v anketi v tem forumu
Ne, ne moreš pripeti datotek v tem forumu
Ne, ne moreš povleči datotek v tem forumu
|
Uptime: 10 dni
Powered by phpBB © 2001, 2005 phpBB Group
|

















